拉曼光谱仪或荧光显微镜中激光光斑尺寸的影响因素分析-仪器仪表网

　　【仪器仪表网 专题推荐】在显微拉曼光谱仪或荧光显微镜中，激光的光斑尺寸大小是一个重要参数，它取决于激光的波长和显微镜的物镜的特性。

　　艾里斑

　　当光穿过任何孔径(例如显微镜物镜)时，就会发生衍射。由均匀照射圆形光圈所产生的衍射图称为艾里斑图(Airy pattern)，如图1所示。它由一个明亮的中心圆(称为艾里斑)组成，包含总光强的84%，其余的16% 分布在一系列逐渐减弱的同心环上。

　　图1. 激光光斑的艾里斑模拟图和光斑尺寸的不同定义。

　　艾里斑的直径(定义为衍射图样中zui小圆斑的直径)通常是显微镜中“光斑大小”的意思。其直径大小取决于激光的波长和物镜的数值孔径(NA)：

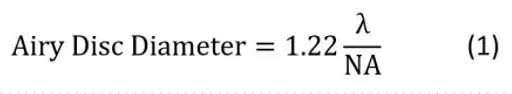
　　显微镜的横向空间分辨率极限与等式1密切相关，通过将系数1.22替换0.61即可。

　　艾里斑直径不是光斑尺寸的weiyi定义。另外两个常见的定义是衍射图样中光斑在半峰宽(FWHM)或1 / e2峰宽时的大小，由下式：

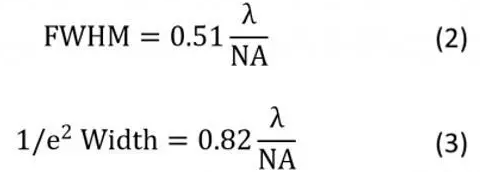
　　艾里圆斑是在假定没有像差的完美光学系统下代表可以达到的zui小光斑尺寸，在实际中很难达到。激光的光束直径通常比物镜的后孔径窄，并且没有均匀的横向强度(通常具有高斯分布)，并且用激光直接照射物镜会导致光斑尺寸大于等式1所预测的。

　　解决的办法是扩大激光束，使其光束直径大于目标物的后孔径，达到近似均匀的照明，这就是所谓的过度填充。过度填充的程度越大，就越接近均匀照明，光斑的大小也越接近公式1。过度填充是以降低到达样品的激光强度为代价的，并且是在空间分辨率和通过物镜传输的功率间做选择。

　　激光波长的影响

　　光斑大小取决于激光波长(公式1)，较短的波长激光器提供较小的光斑和更高的空间分辨率。使用高倍的物镜(100x 0.9 NA)，可以在三种常见的波长下获得光斑大小如图2所示。

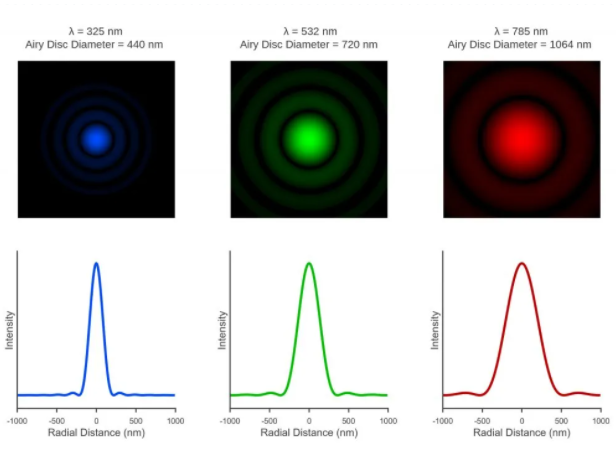
　　图2. 在100x0.9NA物镜下不同波长的光源对应的光斑大小模拟图。

　　物镜的NA值影响

　　光斑的大小还取决于物镜的数值孔径(NA)，该数值孔径测量的是光线进入或离开透镜的倾斜度，

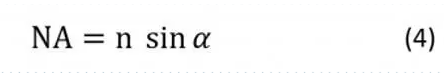
　　其中n是物镜和样品之间介质的折射率，α是进入/出射物镜的光锥的半角。

　　NA取决于物镜的构造，并且通常随物镜放大倍数的增加而增加。标准空气(n = 1)物镜的NA极限值<1，由于浸油物镜的折射率较高，因此可以将NA提高到约1.4。NA越高，物镜的收光角越大，可以实现的光斑尺寸越小，这在图3中用三个常用的空气物镜进行了说明。

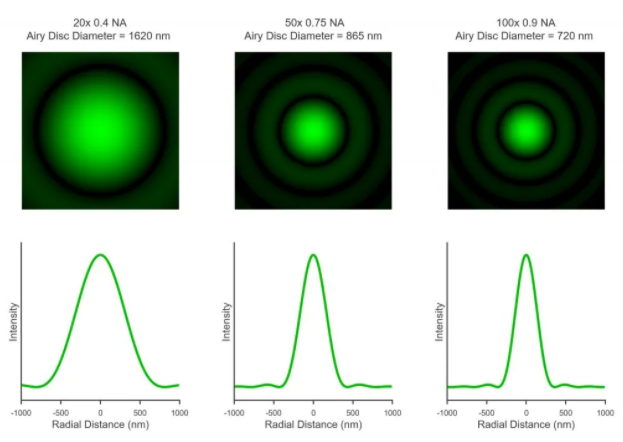
　　图3.模拟在物镜的数值孔径不同情况下532nm激光光斑大小。

　　需要注意的是，图3在某种程度上进行了简化，因为模拟假设所有三个物镜的后孔径均被均匀照明。如上所述，这是通过光束扩展和过度填充物镜的后孔来实现的。但是，后孔径的直径随物镜放大倍数而变化，即后孔径的直径随放大倍率的增加而减小。在多物镜系统中，光束扩展通常是针对高放大倍率物镜进行优化的，而具有较大后孔径的低放大倍率物镜(例如，图3中的20X0.4NA)通常不会被过度填充，并且激光的光斑尺寸和衍射图将会有更多的高斯特性。